9.2 Modelo de reflexão de Phong

O modelo de reflexão de Phong (Phong 1973) modela de forma empírica a quantidade de luz refletida de um ponto \(P\) de uma superfície em uma direção \(\hat{\mathbf{v}}\) até a câmera. O modelo não é baseado na física e, por exemplo, não respeita a lei de conservação de energia. Entretanto, é capaz de produzir a percepção de superfícies iluminadas de uma forma muito eficiente.

A figura 9.5 ilustra a geometria do modelo de reflexão de Phong considerando apenas uma fonte de luz.

Geometria do modelo de reflexão de Phong.

Figura 9.5: Geometria do modelo de reflexão de Phong.

Nessa figura, \(P\) é o ponto de uma superfície, e \(\hat{\mathbf{n}}\) é o vetor normal unitário correspondente.

A luz que incide sobre \(P\) vem de uma direção \(-\hat{\mathbf{l}}\), onde

\[\hat{\mathbf{l}}=\frac{L-P}{|L-P|}\]

é o vetor que vai de \(P\) até a fonte de luz situada em um ponto \(L\), mas normalizado para se transformar em um vetor unitário.

Parte da luz incidente em \(P\) é refletida na direção do vetor

\[\hat{\mathbf{v}}=\frac{E-P}{|E-P|},\]

que é o vetor normalizado de \(P\) até a câmera posicionada em um ponto \(E\).

A intensidade da luz refletida na direção \(\hat{\mathbf{v}}\) é calculada como a soma de três componentes de reflexão: ambiente (\(\mathbf{I}_a\)), difusa (\(\mathbf{I}_d\)) e especular (\(\mathbf{I}_s\)):

\[ \mathbf{I}=\mathbf{I}_a + \mathbf{I}_d + \mathbf{I}_s. \]

A figura 9.6 mostra um exemplo da contribuição de cada componente para a formação da renderização do modelo Stanford Bunny.

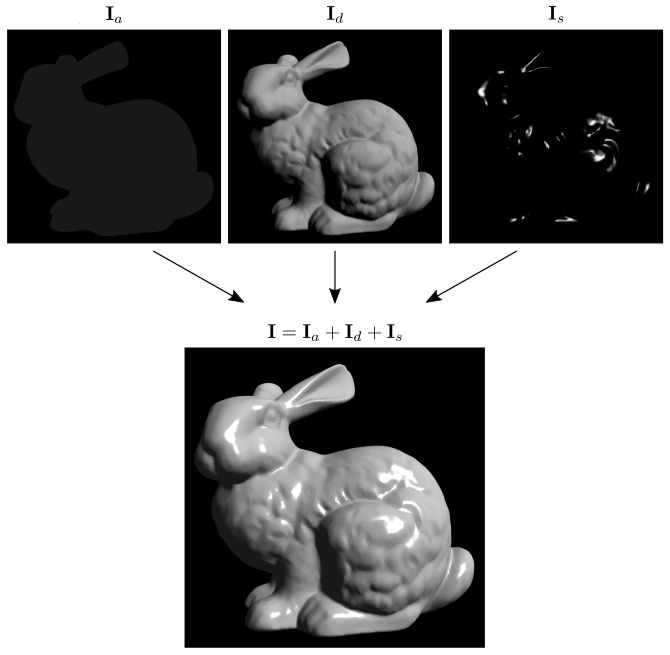
Soma das componentes de reflexão ambiente, difusa e especular.

Figura 9.6: Soma das componentes de reflexão ambiente, difusa e especular.

Nessa imagem, o coelho está centralizado na origem do espaço do mundo. A câmera está em \(E=(0,0,2)\) olhando da direção de \(z\) negativo, e a fonte de luz está localizada em \(L=(100,100,100)\) (acima, à direita e à frente do coelho).

O aspecto de material feito de plástico é característico de superfícies iluminadas com o modelo de reflexão de Phong.

Em geral, uma cena possui mais de uma fonte de luz. Nesse caso, as componentes \(\mathbf{I}_d\) e \(\mathbf{I}_s\) devem ser calculadas para cada fonte de luz e então somadas. Se a cena tiver \(m\) fontes de luz (figura 9.7), então a reflexão deverá ser calculada como

\[ \mathbf{I}=\mathbf{I}_a + \sum_{i=1}^m \left( \mathbf{I}_{d_i} + \mathbf{I}_{s_i} \right). \]

Geometria do modelo de reflexão de Phong para a interação com várias fontes de luz.

Figura 9.7: Geometria do modelo de reflexão de Phong para a interação com várias fontes de luz.

A seguir, detalharemos as componentes de reflexão ambiente, difusa e especular.

Reflexão ambiente

A componente de reflexão ambiente é uma constante que procura aproximar a iluminação indireta resultante das interreflexões de luz entre as superfícies. A componente não depende da posição de \(P\), da posição da câmera \(E\) ou das fontes de luz \(L_1, L_2, \dots, L_m\), e é computada simplesmente como

\[\mathbf{I}_a=\kappa_a \iota_a,\]

onde

  • \(\kappa_a\) é a constante de reflexão ambiente que determina o quanto o material reflete a luz ambiente.
  • \(\iota_a\) é a intensidade de luz ambiente incidente em \(P\).

Uma vez que \(\mathbf{I}_a\) é constante para todos os pontos de um objeto, esse valor pode ser pré-calculado e reutilizado em todos os pontos.

Na maioria das aplicações, \(\mathbf{I}_a\) é um valor bastante baixo. A figura 9.8 mostra o resultado da renderização usando apenas a componente de reflexão ambiente, com \(\kappa_a=1.0\) e \(\iota_a=0.1\). O objeto é desenhado com um tom de cinza, que neste caso é a cor RGB \((0.1, 0.1, 0.1)\), isto é, cada componente de cor é o próprio valor \(\mathbf{I}_a\).

Renderização usando apenas a componente ambiente.

Figura 9.8: Renderização usando apenas a componente ambiente.

Mais adiante descreveremos como estender o cálculo de reflexão para gerar cores em vez de tons de cinza.

Reflexão difusa

A componente de reflexão difusa \(\mathbf{I}_d\) representa a luz que é refletida supondo que \(P\) faz parte de uma superfície difusa ideal, também chamada de superfície lambertiana em homenagem ao matemático e físico suíço Johann Heinrich Lambert (1728–1777), que introduziu tal conceito.

Não há superfícies idealmente difusas no mundo físico. Entretanto, aproximações incluem, por exemplo, paredes de gesso e argamassa, e superfícies em geral que possuem aspecto fosco. Superfícies difusas são aquelas que não possuem brilho especular.

Em uma superfície lambertiana, a luz que incide sobre \(P\) é refletida igualmente em todas as direções, como ilustra a figura 9.9.

Reflexão difusa ideal.

Figura 9.9: Reflexão difusa ideal.

A intensidade da luz refletida é proporcional ao cosseno do ângulo entre \(\hat{\mathbf{l}}\) e \(\hat{\mathbf{n}}\) (relação chamada de lei do cosseno de Lambert), que é o mesmo que o produto escalar entre os vetores unitários:

\[\cos \theta = \hat{\mathbf{l}} \cdot \hat{\mathbf{n}}.\]

Observe que esse valor é também a projeção escalar de \(\hat{\mathbf{l}}\) sobre \(\hat{\mathbf{n}}\).

Quanto maior o ângulo entre \(\hat{\mathbf{l}}\) e \(\hat{\mathbf{n}}\), menor a intensidade da reflexão difusa. A intensidade é mínima quando os vetores são perpendiculares, pois \(\cos(\pi/2) = 0\), e máxima quando paralelos, pois \(\cos(0)=1\). Isso ocorre porque a energia luminosa que incide sobre uma área da superfície é mais concentrada quanto mais perpendicular a luz estiver em relação à superfície (figura 9.10).

A concentração da luz em uma superfície depende da orientação da luz em relação à superfície.

Figura 9.10: A concentração da luz em uma superfície depende da orientação da luz em relação à superfície.

Esse fator de atenuação da reflexão da luz está presente na equação de renderização, através do termo \(\cos \theta_i\) da integral:

\[ I_r(\mathbf x, \omega_{\text{o}}) = I_{\text{e}}(\mathbf x, \omega_{\text{o}}) \ + \int_{\Omega} f_{\text{r}}(\omega_{\text{i}}, \omega_{\text{o}}) I_i(\mathbf x, \omega_{\text{i}}) \cos \theta_i \;\mathrm{d} \omega_{\text{i}}. \]

Em uma superfície idealmente difusa, a BRDF é uma constante, isto é, \(f_r(\omega_i,\omega_o)=\kappa_d\). Logo, a equação de renderização torna-se

\[ \begin{align} I_r(\mathbf x, \omega_{\text{o}}) &= I_{\text{e}}(\mathbf x, \omega_{\text{o}}) \ + \int_{\Omega} \kappa_d I_i(\mathbf x, \omega_{\text{i}}) \cos \theta_i \;\mathrm{d} \omega_{\text{i}}\\ &= I_{\text{e}}(\mathbf x, \omega_{\text{o}}) \ + \kappa_d \int_{\Omega} I_i(\mathbf x, \omega_{\text{i}}) \cos \theta_i \;\mathrm{d} \omega_{\text{i}}. \end{align} \]

O modelo de reflexão de Phong aproxima isso calculando a componente difusa como

\[ \mathbf{I}_d = \kappa_d \iota_{d} (\hat{\mathbf{l}} \cdot \hat{\mathbf{n}}), \]

onde

  • \(\kappa_d\) é a constante de reflexão difusa que determina o quanto o material reflete a luz difusa.
  • \(\iota_d\) é a intensidade de luz difusa incidente em \(P\).
  • \(\hat{\mathbf{l}} \cdot \hat{\mathbf{n}}\) é o fator de atenuação relacionado à lei de cosseno de Lambert. São válidos apenas os valores no intervalo \([0,1]\).

A figura 9.11 mostra o resultado da renderização usando apenas a componente de reflexão difusa, com \(\kappa_d=0.7\) e \(\iota_d=1.0\).

Renderização usando apenas a componente difusa.

Figura 9.11: Renderização usando apenas a componente difusa.

Se tivermos \(m>1\) fontes de luz, cada fonte de luz terá seu próprio vetor \(\hat{\mathbf{l}}\) e sua própria intensidade \(\iota_{d}\). A componente \(\mathbf{I}_d\) deverá levar em conta a soma de todas essas intensidades:

\[ \mathbf{I}_d = \kappa_d \sum_{i=1}^m \iota_{d_i} (\hat{\mathbf{l}}_i \cdot \hat{\mathbf{n}}). \]

Observação

  • Note a semelhança entre \(\mathbf{I}_d\) e a integral da equação de renderização com BRDF constante:

    \[\kappa_d \sum_{i=1}^m \iota_{d_i} (\hat{\mathbf{l}}_i \cdot \hat{\mathbf{n}}) \approx \kappa_d \int_{\Omega} I_i(\mathbf x, \omega_{\text{i}}) \cos \theta_i \;\mathrm{d} \omega_{\text{i}}.\]

    • A integral é substituída pelo somatório, pois as fontes de luz podem ser consideradas como pontos discretos no espaço;
    • \(\iota_{d_i}\) é uma aproximação de \(I_i(\mathbf x, \omega_{\text{i}})\) para a incidência da luz da \(i\)-ésima fonte de luz;
    • \(\hat{\mathbf{l}}_i \cdot \hat{\mathbf{n}}\) é \(\cos \theta_i\).

  • Note também que \(\mathbf{I}_d\) não usa o vetor \(\hat{\mathbf{v}}\), que é o vetor de direção até a câmera. Isso significa que a componente de reflexão difusa não depende da posição da câmera.

    Se a cena é estática, isto é, se os objetos e as fontes de luz não se movem, a componente de reflexão difusa de cada ponto pode ser pré-calculada. Essa característica é explorada na técnica de radiosidade (Greenberg, Cohen, and Torrance 1986). A técnica considera que todas as superfícies da cena são lambertianas. Desse modo, a solução da equação de renderização pode ser pré-computada e a intensidade de reflexão difusa pode ser gravada como a “cor” de cada vértice. A cena pode então ser visualizada por uma câmera LookAt em tempo real.

Reflexão especular

Uma superfície idealmente especular é um espelho ideal. A luz que incide em \(P\) é refletida apenas na direção reflexa \(\hat{\mathbf{r}}\) do vetor \(\hat{\mathbf{l}}\) em torno de \(\hat{\mathbf{n}}\), como mostra a figura 9.12.

Reflexão especular ideal.

Figura 9.12: Reflexão especular ideal.

O vetor \(\hat{\mathbf{r}}\) de reflexão ideal é calculado como

\[ \hat{\mathbf{r}} = 2(\hat{\mathbf{l}} \cdot \hat{\mathbf{n}})\hat{\mathbf{n}} - \hat{\mathbf{l}}. \]

A figura 9.13 mostra uma interpretação geométrica desssa expressão.

Calculando o vetor de reflexão especular.

Figura 9.13: Calculando o vetor de reflexão especular.

No modelo de reflexão de Phong, a reflexão especular \(\mathbf{I}_s\) é um valor que varia de acordo com o ângulo formado entre \(\hat{\mathbf{r}}\) e \(\hat{\mathbf{v}}\):

\[ \mathbf{I}_s= \kappa_s \iota_{s} (\hat{\mathbf{r}} \cdot \hat{\mathbf{v}})^\alpha, \]

onde

  • \(\kappa_s\) é a constante de reflexão especular que determina o quanto o material reflete a luz especular.

  • \(\iota_s\) é a intensidade de luz especular incidente em \(P\).

  • \(\alpha \geq 0\) é uma constante que determina o espalhamento do brilho especular. É uma propriedade do material.

    Quanto maior é o valor de \(\alpha\), mais concentrado será o brilho especular. Desse modo, \(\alpha\) define o quão “lustro” é o material. Se \(\alpha=\infty\), o resultado é um superfície especular ideal (espelho ideal).

  • \(\hat{\mathbf{r}} \cdot \hat{\mathbf{v}}\) é o cosseno do ângulo entre \(\hat{\mathbf{r}}\) e \(\hat{\mathbf{v}}\). São válidos apenas os valores no intervalo \([0,1]\).

    O brilho especular é máximo (\(\hat{\mathbf{r}} \cdot \hat{\mathbf{v}}=1\)) se \(\hat{\mathbf{r}}=\hat{\mathbf{v}}\).

    O brilho especular é mínimo (\(\hat{\mathbf{r}} \cdot \hat{\mathbf{v}}=0\)) se \(\hat{\mathbf{r}}\) e \(\hat{\mathbf{v}}\) são perpendiculares.

A figura 9.14 mostra o resultado da variação do brilho especular para diferentes valores de \(\alpha\) e ilustra a variação correspondente de \(\hat{\mathbf{r}} \cdot \hat{\mathbf{v}}\). As renderizações consideram os valores de intensidade ambiente e difusa mostrados nas figuras 9.8 e 9.11.

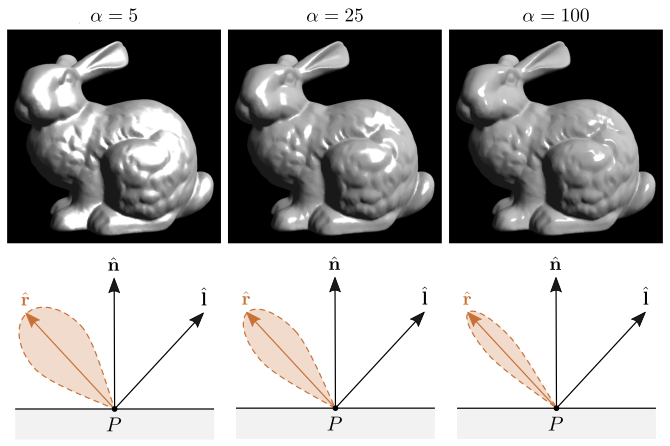
Renderização usando diferentes valores de brilho especular.

Figura 9.14: Renderização usando diferentes valores de brilho especular.

A figura 9.15 mostra o resultado da renderização usando apenas a componente de reflexão especular, com \(\kappa_s=0.7\) e \(\iota_s=1.0\) e \(\alpha=50\).

Renderização usando apenas a componente especular.

Figura 9.15: Renderização usando apenas a componente especular.

Se tivermos \(m>1\) fontes de luz, cada fonte de luz terá seu próprio vetor \(\hat{\mathbf{r}}\) e sua própria intensidade \(\iota_{s}\). A componente \(\mathbf{I}_s\) deverá levar em conta a soma de todas essas intensidades:

\[ \mathbf{I}_s = \kappa_s \sum_{i=1}^m \iota_{s_i} (\hat{\mathbf{r}}_i \cdot \hat{\mathbf{v}})^\alpha. \]

Modelo completo

Combinando as componentes ambiente, difusa e especular, temos a equação completa

\[ \mathbf{I}=\kappa_a \iota_a + \sum_{i=1}^m \left(\kappa_d \iota_{d_i} (\hat{\mathbf{l}}_i \cdot \hat{\mathbf{n}}) + \kappa_s \iota_{s_i} (\hat{\mathbf{r}}_i \cdot \hat{\mathbf{v}})^\alpha\right). \]

A equação pode ser avaliada em um vertex shader ou fragment shader, pois podemos armazenar as seguintes informações como variáveis uniformes (uniform):

  • \(\alpha\) (constante de espalhamento de brilho especular).
  • \(m\) (número de fontes de luz).
  • \(\kappa_a\), \(\kappa_d\), \(\kappa_s\) (coeficientes de reflexão do material).
  • \(\iota_d\), \(\iota_s\) (intensidades de luz difusa e especular, em um arranjo de \(m\) elementos, um para cada fonte de luz).
  • \(\iota_a\) (intensidade de luz ambiente).

Além disso, \(\hat{\mathbf{n}}\) pode ser pré-calculado como um atributo do vértice, isto é, como um VBO de vetores normais de vértices.

Podemos calcular \(\hat{\mathbf{l}}\) como

\[\hat{\mathbf{l}}=\frac{L-P}{|L-P|},\]

onde \(L\) é a posição da fonte de luz, que também pode ser armazenada como uma variável uniforme, e \(P\) é o atributo de posição do vértice atual (caso a equação seja avaliada no vertex shader) ou fragmento atual (caso a equação seja avaliada no fragment shader).

Podemos calcular \(\hat{\mathbf{v}}\) como

\[\hat{\mathbf{v}}=\frac{E-P}{|E-P|},\] onde \(E\) é a posição da câmera. Se considerarmos que \(P\) está no espaço da câmera, então a posição da câmera é a origem:

\[E=(0,0,0)\] e assim não é necessário enviar \(E\) ao shader como uma variável uniforme.

Como já vimos, \(\hat{\mathbf{r}}\) pode ser calculado como

\[\hat{\mathbf{r}} = 2(\hat{\mathbf{l}} \cdot \hat{\mathbf{n}})\hat{\mathbf{n}} - \hat{\mathbf{l}}.\]

Enfim, temos tudo o que é preciso para implementar o modelo de reflexão de Phong no pipeline gráfico. Faremos isso em um passo a passo de implementação nas seções 9.5 e 9.6.

Iluminação colorida

Até agora só consideramos fontes de luz e materiais monocromáticos. Se quisermos representar fontes de luz coloridas ou materiais coloridos, devemos calcular \(\mathbf{I}\) para cada uma das componentes RGB. Assim, as constantes de material (\(\kappa_a\), \(\kappa_d\), \(\kappa_s\)) e as intensidades (\(\iota_a\), \(\iota_d\), \(\iota_s\)) deverão ser tuplas de três elementos:

\[ \kappa_a=(\kappa_{a,r}, \kappa_{a,g}, \kappa_{a,b}),\\ \kappa_d=(\kappa_{d,r}, \kappa_{d,g}, \kappa_{d,b}),\\ \kappa_s=(\kappa_{s,r}, \kappa_{s,g}, \kappa_{s,b}), \]

e

\[ \iota_a=(\iota_{a,r}, \iota_{a,g}, \iota_{a,b}),\\ \iota_d=(\iota_{d,r}, \iota_{d,g}, \iota_{d,b}),\\ \iota_s=(\iota_{s,r}, \iota_{s,g}, \iota_{s,b}). \]

Os elementos dessas tuplas correspondem a cores RGB. Por exemplo, um objeto de cor vermelha poderá ser especificado com um material com constante de reflexão difusa

\[ \kappa_d=(1,0,0). \]

Isso significa que o material reflete toda luz vermelha (\(\kappa_{d,r}=1\)) e absorve completamente as outras cores (\(\kappa_{d,g}=\kappa_{d,b}=0\)) das fontes de luz.

Alguns exemplos de materiais são mostrados na figura 9.16. Todos esses materiais estão sendo iluminados por uma fonte de luz branca, \(\iota_d=\iota_s=(1,1,1)\). A luz ambiente também é branca com intensidade máxima (\(\iota_a=(1,1,1)\)).

Diferentes materiais no modelo de Phong.

Figura 9.16: Diferentes materiais no modelo de Phong.

Como regra geral, se o material não é um metal, \(\kappa_s\) deve ter o mesmo valor para cada componente RGB, pois a cor do brilho especular deve ser a cor da fonte de luz. Se o material é um metal, \(\kappa_s\) deve ser a cor do material. Por exemplo, em um objeto feito de ouro, a cor especular deve ser amarelada.

A cor de uma fonte de luz pode ser especificada através da intensidade de luz difusa. Por exemplo, uma luz verde é definida com

\[ \iota_d=(0,1,0). \]

Suponha que a luz verde ilumine um material vermelho com \(\kappa_d=(1,0,0)\). O resultado de \(\kappa_d\iota_d\) (multiplicação elemento a elemento) será a cor preta

\[ \kappa_d\iota_d = (0,0,0). \]

Isso faz sentido pois, de fato, um objeto vermelho têm a aparência de um objeto preto quanto iluminado por uma luz verde.

Fontes de luz

Até agora, consideramos que cada fonte de luz do modelo de reflexão de Phong é um ponto \(L\) no espaço. Essa é a definição de uma fonte de luz pontual.

Além da luz pontual, também é comum o uso de luz direcional. A seguir, definiremos a luz direcional e revisitaremos a definição de luz pontual com a introdução do conceito adicional de atenuação espacial.

Luz pontual

Uma fonte de luz pontual é definida por um ponto que emite luz em igual intensidade em todas as direções, como uma lâmpada tradicional de bulbo.

Se \(L\) é a posição da luz, então o vetor \(\hat{\mathbf{l}}\) do modelo de reflexão é definido como

\[\hat{\mathbf{l}}=\frac{L-P}{|L-P|}.\]

Podemos simular um efeito de atenuação da luz, isto é, diminuição da intensidade da fonte de luz de acordo com a distância do ponto \(L\) em relação ao ponto \(P\).

As intensidades que devem ser atenuadas são as contantes \(\iota_d\) (intensidade difusa) e \(\iota_s\) (intensidade especular). Opcionalmente, podemos atenuar \(\iota_a\) (intensidade ambiente) caso consideremos que a fonte de luz em questão contribui para a intensidade ambiente.

No mundo físico, a intensidade da luz trasmitida no vácuo é proporcional ao inverso da distância ao quadrado. Entretanto, podemos obter um maior controle artístico se considerarmos que o fator de atenuação é definido de forma mais geral como:

\[ F_{\textrm{att}}=\frac{1}{k_c+k_ld+k_qd^2}. \]

onde

  • \(d\) é a distância, isto é, \(|L-P|\).
  • \(k_c\), \(k_l\) e \(k_q\) são, respectivamente, os termos constante, linear e quadrático da atenuação. Esses valores devem estar no intervalo \([0,1]\).

Em geral, \(k_c=1\) para evitar que o valor de atenuação seja maior que \(1\).

Geralmente, \(k_l\leq 1\) e \(k_q \leq 1\), mas a escolha dos valores dependerá do efeito desejado. Um bom ponto de partida é começar com \(k_l=k_q=0.2\). Isso faz com que a fonte de luz ilumine objetos até aproximadamente \(d=20\). Quanto menor o valor de \(k_l\) e \(k_q\), maior a distância coberta pela fonte de luz.

Se considerarmos que todas as fontes de luz são pontuais e atenuadas, podemos reformular o modelo de reflexão como a seguir:

\[ \mathbf{I}=\kappa_a \iota_a + \sum_{i=1}^m F_{\textrm{att}_i}\left(\kappa_d \iota_{d_i} (\hat{\mathbf{l}}_i \cdot \hat{\mathbf{n}}) + \kappa_s \iota_{s_i} (\hat{\mathbf{r}}_i \cdot \hat{\mathbf{v}})^\alpha\right), \]

onde \(F_{\textrm{att}_i}\) é o fator de atenuação da \(i\)-ésima fonte de luz.

Luz direcional

A fonte de luz direcional simula o comportamento de uma fonte de luz pontual infinitamente distante, de tal modo que os raios de luz que chegam à superfície são paralelos entre si. No mundo físico, uma aproximação de fonte de luz direcional é a luz do sol.

A luz direcional é definida simplesmente por um vetor \(\mathbf{u}\) de direção da luz. Como não há posição do espaço, não há como calcular a atenuação.

Dada uma direção \(\mathbf{u}\) de luz direcional, o vetor \(\hat{\mathbf{l}}\) do modelo de reflexão de Phong é definido como

\[\hat{\mathbf{l}}=-\frac{\mathbf{u}}{|\mathbf{u}|}.\]

Luz spot

Uma luz do tipo spot (spotlight) é um tipo de luz pontual na qual a luz é emitida apenas em um facho cônico de luz em torno de uma direção central. A luz spot é definida pelos seguintes parâmetros (figura 9.17):

  • Uma posição \(L\), como na luz pontual.
  • Uma direção \(\hat{\mathbf{u}}\) que corresponde à direção (normalizada) do centro do facho de luz.
  • Um ângulo de corte \(\phi \in [0, \pi]\) que corresponde ao ângulo entre a direção \(\mathbf{u}\) e a borda do cone.
Parâmetros de uma fonte de luz spot.

Figura 9.17: Parâmetros de uma fonte de luz spot.

Se \(P\) é um ponto na superfície, então

\[\hat{\mathbf{l}}=\frac{L-P}{|L-P|},\] e \(P\) está iluminado pela luz spot se

\[\cos{\theta} > \cos{\phi},\] onde \[\cos{\theta}=\hat{\mathbf{u}} \cdot -\hat{\mathbf{l}}.\]

Se \(P\) está iluminado, a intensidade de luz em \(P\) é calculada como no caso da luz pontual. Se \(P\) não está iluminado, a intensidade de luz em \(P\) será nula para esta fonte de luz.

Referências

Greenberg, Donald P., Michael F. Cohen, and Kenneth E. Torrance. 1986. “Radiosity: A Method for Computing Global Illumination.” The Visual Computer 2 (5): 291–97. https://doi.org/10.1007/BF02020429.
Phong, Bui Tuong. 1973. “Illumination of Computer-Generated Images.” Technical Report UTEC-CSs-73-129. University of Utah.