10.6 Mapeamento de ambiente

No modelo de reflexão de Phong e Blinn-Phong, a cor calculada em um ponto da superfície é determinada unicamente pela luz que incide diretamente sobre o ponto. A iluminação indireta, isto é, a luz refletida de outros objetos, é ignorada. Uma consequência disso é que não é possível representar superfícies que refletem o ambiente ao seu redor. Entretanto, a aparência de objetos reflexivos pode ser obtida através da técnica de mapeamento de ambiente.

Mapeamento de ambiente (environment mapping) é uma técnica de texturização que aproxima a aparência de superfícies reflexivas.

O exemplo interativo a seguir usa mapeamento de ambiente (mais especificamente, mapeamento cúbico) para simular uma superfície reflexiva. Use o botão esquerdo do mouse para rodar o objeto, e o botão direito para rodar o ambiente exibido como textura de fundo:

A ideia principal do mapeamento de ambiente consiste na definição de uma correspondência entre as coordenadas de um vetor 3D sobre um ponto da superfície – geralmente o vetor de reflexão ideal \(\hat{\mathbf{r}}\) – e as coordenadas de uma textura que representa o ambiente ao redor do ponto. O valor amostrado corresponde à iluminação ambiente refletida pela superfície.

Para simplificar, geralmente supõe-se que o ambiente está a uma distância infinita da superfície. Desse modo, o resultado não depende da translação do objeto que está sendo renderizado. Além disso, é comum supor que o ambiente é estático de modo que o mapa de ambiente pode ser preprocessado.

Há inúmeras variações de mapeamento de ambiente, cada uma com suas vantagens e desvantagens. Na discussão a seguir nos limitaremos a três dessas variações:

• Mapeamento de ambiente esférico (sphere mapping).
• Mapeamento de ambiente equiretangular (equirectangular mapping).
• Mapeamento de ambiente cúbico (cube mapping).

Mapeamento de ambiente esférico

No mapeamento esférico, usa-se um mapa de textura esférico (sphere map) que contém a representação 2D de uma visão de \(360^{\circ}\) do ambiente. A figura 10.26 mostra um exemplo de mapa esférico.

Figura 10.26: Mapa de ambiente esférico (adaptado do original).

Se o vetor de reflexão ideal de um ponto \(P\) de uma superfície tem coordenadas \(\hat{\mathbf{r}}=(x, y, z)\) no espaço da câmera, as respectivas coordenadas de textura no mapa esférico são calculadas como

\[ u=\frac{1}{2}\left(\frac{x}{m}+1\right),\\ v=\frac{1}{2}\left(\frac{y}{m}+1\right), \]

onde

\[ m=\sqrt{x^2+y^2+(z+1)^2}. \]

O valor resultante do mapa esférico amostrado em \((u,v)\) é a intensidade de cor do ambiente refletida em \(P\).

Embora o mapeamento entre o vetor unitário de coordenadas \((x,y,z)\) e as coordenadas de textura \((u,v)\) seja simples, o mapeamento de ambiente esférico possui várias limitações:

• O mapa de textura esférico não é independente da direção de visão e precisa ser reconstruído sempre que a câmera mudar de orientação.
• A representação 2D da visão de \(360^{\circ}\) pode introduzir distorções severas no mapeamento do ambiente. O texel em \((u,v)=(0.5, 0.5)\), correpondente ao vetor \((0,0,1)\) no espaço da câmera, não tem distorção. Porém, a distorção aumenta quanto mais o vetor aproxima-se de \((0,0,-1)\). A direção \((0,0,-1)\) não tem representação no mapa esférico e corresponde a uma singularidade no mapeamento.
• Há desperdício de memória pois os texels situados fora do círculo não são utilizados.

Os mapeamentos de ambiente equiretangular e cúbico são independentes da direção de visão e geram menos distorções. Por isso, substituem o mapeamento de ambiente esférico na maioria das aplicações.

Mapeamento de ambiente equiretangular

O mapeamento de ambiente equiretangular usa mapas de textura com projeção cilíndrica equidistante, como o mapa exibido na figura 10.27. Essa projeção é conhecida por seu uso em cartografia (projeção de Plate Carrée) e em fotografia panorâmica.

Figura 10.27: Mapa de ambiente equiretangular (fonte).

A projeção equiretangular converte coordenadas esféricas em coordenadas planares de tal modo que a coordenada \(u\) é mapeada para a longitude, \(v\) é mapeada para a longitude, e a distância entre os meridianos (pontos de mesmo valor \(u\)) e entre os paralelos (pontos de mesmo valor \(v\)) em intervalos regulares é sempre a mesma. Essa é a mesma projeção utilizada no mapeamento esférico visto na seção 10.1. Assim, para um dado ponto \(P\) com vetor de reflexão ideal \(\hat{\mathbf{r}}=(x, y, z)\) no espaço da câmera, as coordenadas de textura correspondentes no mapa equiretangular são calculadas como:

\[ \begin{align*} u&=\frac{\arctan2(x, z)}{2\pi} + 0.5,\\ v&=\frac{\arcsin(y)}{\pi} + 0.5. \end{align*} \]

O mapeamento de ambiente equiretangular não produz as distorções do mapeamento de ambiente esférico. Além disso, o mapa não precisa ser reconstruído para cada nova direção de visão. Porém, ainda há algumas desvantagens. Uma delas é o desperdício de memória na representação de pixels fora da linha do equador (linha horizontal na metade do mapa de textura). Quanto mais próximo dos polos, mais os pixels se repetem. O número de pixels não repetidos é proporcional ao cosseno do ângulo de latitude, sendo máximo no equador (1), e mínimo (0) na primeira e na última linha do mapa, quando todos os pixels da linha possuem o mesmo valor.

Outra desvantagem do mapeamento de ambiente equiretangular é o custo computacional decorrente do uso de funções transcedentais para converter as coordenadas do vetor de reflexão em coordenadas do mapa de textura.

Veremos a seguir o mapeamento de ambiente cúbico, que resolve essas limitações e, por isso, é o mais utilizado em aplicações de computação gráfica em tempo real.

Mapeamento de ambiente cúbico

O mapeamento de ambiente cúbico considera que cada ponto da superfície está situado no centro de um cubo imaginário que representa o ambiente ao redor do ponto. Cada lado do cubo corresponde a uma textura, de modo que qualquer direção no \(\mathbb{R}^3\) pode ser mapeada para uma posição única em alguma das seis texturas (figura 10.28).

Figura 10.28: Cada direção corresponde a um par de coordenadas de textura em um dos lados do cubo.

A coleção de seis texturas, uma para cada lado do cubo, é chamada de mapa de textura cúbico (cubemap). A figura 10.29 mostra um exemplo de mapa de textura cúbico e seu mapeamento no cubo imaginário. Segundo a convenção adotada pelo OpenGL, o cubo é definido em um sistema que segue a regra da mão esquerda.

Figura 10.29: Mapa de ambiente cúbico mapeado sobre as faces internas de um cubo (mapa de textura por Emil Persson).

Reflexão

Para aproximar uma superfície reflexiva, a direção do vetor \(\hat{\mathbf{r}}=(x,y,z)\) calculado sobre um ponto \(P\) da superfície é mapeada para coordenadas de textura \((u,v)\) em uma das seis texturas do mapa cúbico. O resultado da amostragem é a intensidade de luz do ambiente refletida por \(P\) (figura 10.30).

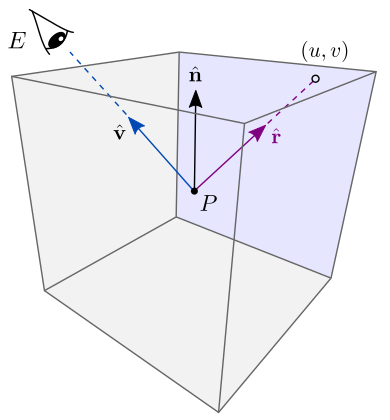
Figura 10.30: Mapeamento cúbico usando o vetor de reflexão ideal.

As coordenadas de textura são calculadas como

\[ u=\frac{1}{2}\left(\frac{u_c}{m}+1\right),\\ v=\frac{1}{2}\left(\frac{v_c}{m}+1\right), \]

onde

\[ m = \text{max}\{|x|, |y|, |z|\}, \]

e

\[ (u_c, v_c) = \begin{cases} (-z,-y) \quad\text{na textura +x} &\text{se}\quad x>0 \quad\text{e}\quad m=|x|, \\ (\phantom{-}z,-y) \quad\text{na textura}-\hspace{-0.25em}\text{x} &\text{se}\quad x\leq0 \quad\text{e}\quad m=|x|, \\ (\phantom{-}x,\phantom{-}z) \quad\text{na textura +y} &\text{se}\quad y>0 \quad\text{e}\quad m=|y|, \\ (\phantom{-}x,-z) \quad\text{na textura}-\hspace{-0.25em}\text{y} &\text{se}\quad y\leq0 \quad\text{e}\quad m=|y|, \\ (\phantom{-}x,-y) \quad\text{na textura +z} &\text{se}\quad z>0 \quad\text{e}\quad m=|z|, \\ (-x,-y) \quad\text{na textura}-\hspace{-0.25em}\text{z} &\text{se}\quad z\leq0 \quad\text{e}\quad m=|z|. \end{cases} \]

Refração

Refração é o fenômeno de mudança na direção de propagação da luz quando a luz transmitida por um meio muda para outro meio (por exemplo, do ar para a água). A figura 10.31 ilustra como a luz na direção \(\hat{\mathbf{i}}\) propagada no ar muda para uma direção \(\hat{\mathbf{t}}\) ao atravessar a superfície de diferentes materiais (água, vidro e diamante).

Figura 10.31: Refração em diferentes meios.

A relação entre o ângulo \(\theta_1\) (ângulo de incidência) e o ângulo \(\theta_2\) (ângulo de refração), é dada pela Lei de Snell:

\[ \frac{\sin{\theta_1}}{\sin{\theta_2}}=\frac{n_1}{n_2}, \]

onde \(n_1\) e \(n_2\) são os índices de refração dos meios.

A tabela 10.1 mostra os índices de refração de alguns materiais.

Tabela 10.1: Índices de refração.

Meio	Índice de refração
Ar	1.00
Água	1.33
Gelo	1.31
Vidro	1.52
Diamante	2.42

O mapeamento de ambiente pode ser utilizado para simular o efeito de refração. Para isto, considera-se que o vetor \(\hat{\mathbf{i}}\) de luz incidente é a direção oposta do vetor até o observador, isto é,

\[ \hat{\mathbf{i}}=-\hat{\mathbf{v}}. \]

Uma vez calculado o vetor \(\hat{\mathbf{t}}\), basta amostrar o mapa de textura cúbico a partir das coordenadas de \(\hat{\mathbf{t}}\) no lugar de \(\hat{\mathbf{r}}\).

A figura 10.32 ilustra a geometria do cálculo do vetor \(\hat{\mathbf{t}}\) a partir do vetor \(\hat{\mathbf{i}}\), vetor \(\hat{\mathbf{n}}\) normal à superfície, e ângulos \(\theta_1\) e \(\theta_2\) de incidência e refração.

Figura 10.32: Geometria do vetor de refração.

O vetor \(\hat{\mathbf{t}}\) pode ser escrito como a soma de dois vetores \(\mathbf{a}\) e \(\mathbf{b}\):

\[ \hat{\mathbf{t}}=\mathbf{a}+\mathbf{b}, \]

onde

\[ \begin{align} &\mathbf{a}=\hat{\mathbf{m}}\sin{\theta_2},\\ &\mathbf{b}=-\hat{\mathbf{n}}\cos{\theta_2}. \end{align} \]

O vetor \(\mathbf{a}\) depende do vetor unitário \(\hat{\mathbf{m}}\) calculado como

\[ \hat{\mathbf{m}}=\dfrac{\hat{\mathbf{i}}+\mathbf{c}}{\sin{\theta_1}}, \]

onde

\[ \mathbf{c}=\hat{\mathbf{n}}\cos{\theta_1}. \]

Observe que \(\hat{\mathbf{i}}+\mathbf{c}\) tem tamanho \(\sin{\theta_1}\). Logo, a divisão por \(\sin{\theta_1}\) resulta no vetor unitário \(\hat{\mathbf{m}}\).

Expandindo a equação \(\hat{\mathbf{t}}=\mathbf{a}+\mathbf{b}\) e combinando com a relação entre os senos dos ângulos (Lei de Snell), é possível chegar à forma simplificada:

\[ \hat{\mathbf{t}}=\eta\hat{\mathbf{i}}+(\eta c_1 - c_2)\hat{\mathbf{n}}, \]

onde \(\eta\) é a razão entre os índices de refração:

\[ \eta = \frac{n_1}{n_2}, \]

e

\[ \begin{align} &c_1=\cos{\theta_1}=\hat{\mathbf{n}}\cdot \hat{\mathbf{i}},\\ &c_2=\cos{\theta_2}=\sqrt{1 - \eta^2\left(1-c_1^2\right)}. \end{align} \]

Mapeamento de ambiente na prática

Vamos continuar com o desenvolvimento do visualizador de modelos 3D, desta vez acrescentando shaders de mapeamento de ambiente cúbico para simular o efeito de reflexão e refração.

Esta será a versão 6 do visualizador (viewer6). Utilizaremos o código do projeto viewer5 apresentado na seção 10.5 e incluiremos os seguintes shaders:

• cubereflect.vert e cubereflect.frag para simular o efeito de reflexão.
• cuberefract.vert e cuberefract.frag para simular o efeito de refração.
• skybox.vert e skybox.frag para mostrar o mapa de textura cúbico como uma textura de fundo;

O resultado ficará como a seguir:

Baixe o código completo deste link.

Carregando o mapa de textura cúbico

Nos projetos anteriores, utilizamos as funções Model::loadDiffuseTexture e Model::loadNormalTexture para carregar as texturas difusa e de normais. Agora, incluiremos a função Model::loadCubeTexture para criar o mapa de textura cúbico:

void Model::loadCubeTexture(std::string const &path) {
  if (!std::filesystem::exists(path))
    return;

  abcg::glDeleteTextures(1, &m_cubeTexture);
  m_cubeTexture = abcg::loadOpenGLCubemap(
      {.paths = {path + "posx.jpg", path + "negx.jpg", path + "posy.jpg",
                 path + "negy.jpg", path + "posz.jpg", path + "negz.jpg"}});
}

A textura é identificada por m_cubeTexture.

Model::loadCubeTexture recebe o caminho de um diretório (path) que deve conter os arquivos posx.jpg, negx.jpg, posy.jpg, negy.jpg, posz.jpg e negz.jpg correspondentes aos arquivos de imagem das texturas de cada lado do cubo. Esses nomes são enviados como um arranjo de strings para o método abcg::loadOpenGLCubemap, definido em abcgOpenGLImage.cpp.

Internamente, abcg::loadOpenGLCubemap cria um identificador de textura e liga-o ao alvo GL_TEXTURE_CUBE_MAP no lugar de GL_TEXTURE_2D:

GLuint textureID{};
glGenTextures(1, &textureID);
glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);

Em seguida, a função glTexImage2D é chamada seis vezes. Cada chamada de glTexImage2D usa como alvo um dos identificadores a seguir que identifica um lado do cubo:

• GL_TEXTURE_CUBE_MAP_POSITIVE_X para o lado +x;
• GL_TEXTURE_CUBE_MAP_NEGATIVE_X para o lado -x;
• GL_TEXTURE_CUBE_MAP_POSITIVE_Y para o lado +y;
• GL_TEXTURE_CUBE_MAP_NEGATIVE_Y para o lado -y;
• GL_TEXTURE_CUBE_MAP_POSITIVE_Z para o lado +z;
• GL_TEXTURE_CUBE_MAP_NEGATIVE_Z para o lado -z.

Consulte a definição de abcg::loadOpenGLCubemap em abcg/abcgOpenGLImage.cpp para mais detalhes.

Voltando agora ao código do visualizador, a função Model::loadCubeTexture é chamada em Window::loadModel:

  m_model.loadCubeTexture(assetsPath + "maps/cube/");

Essa chamada de função supõe que os seis arquivos de imagem estão em assets/maps/cube/.

Em Model::render, precisamos habilitar a unidade de textura que utilizará o mapa de textura cúbico. Nos projetos anteriores, ativamos as unidades GL_TEXTURE0 para a textura difusa, e GL_TEXTURE1 para a textura de normais. Agora, ativaremos a unidade GL_TEXTURE2 para o mapa cúbico:

  abcg::glActiveTexture(GL_TEXTURE0);
  abcg::glBindTexture(GL_TEXTURE_2D, m_diffuseTexture);

  abcg::glActiveTexture(GL_TEXTURE1);
  abcg::glBindTexture(GL_TEXTURE_2D, m_normalTexture);

  abcg::glActiveTexture(GL_TEXTURE2);
  abcg::glBindTexture(GL_TEXTURE_CUBE_MAP, m_cubeTexture);

Com essa configuração, podemos usar até três amostradores de textura ao mesmo tempo no fragment shader: diffuseTex, normalTex, e agora cubeTex. Na verdade, nossos novos shaders (cubereflect.frag e cuberefract.frag) não usam diffuseTex e normalTex. Então, poderíamos deixar o mapa cúbico na unidade GL_TEXTURE0 também.

Há ainda mais um passo necessário para habilitar o uso amostrador no shader. Em Window::onPaint, precisamos definir o valor da variável uniforme cubeTex. Esse valor deve ser 2 pois queremos que essa variável do amostrador use a unidade de textura GL_TEXTURE2. Assim, em Window::onPaint teremos os seguintes trechos de código atualizados:

  auto const cubeTexLoc{abcg::glGetUniformLocation(program, "cubeTex")};

e

  abcg::glUniform1i(cubeTexLoc, 2);

Shaders

Os shaders de reflexão e refração ambiente são bastante similares. Começaremos com o shaders de reflexão ambiente (cubereflect.vert e cubereflect.frag) e em seguida abordaremos os shaders de refração (cuberefract.vert e cuberefract.frag).

Para simplificar, vamos considerar que a cor de cada ponto da superfície do modelo é determinada unicamente pelos valores do mapa de textura cúbico. Em outras palavras, a iluminação e a texturização difusa ou de normais será ignorada.

cubereflect.vert

O código completo do vertex shader é mostrado a seguir:

#version 300 es

layout(location = 0) in vec3 inPosition;
layout(location = 1) in vec3 inNormal;

uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projMatrix;
uniform mat3 normalMatrix;

out vec3 fragP;
out vec3 fragN;

void main() {
  fragP = (viewMatrix * modelMatrix * vec4(inPosition, 1.0)).xyz;
  fragN = normalMatrix * inNormal;

  gl_Position = projMatrix * vec4(fragP, 1.0);
}

Os atributos de entrada são apenas dois:

• inPosition: posição do vértice no espaço do objeto;
• inNormal: vetor normal no espaço do objeto.

Observe que não precisamos das coordenadas de textura, pois elas podem ser calculadas a partir das coordenadas do vetor de reflexão ideal.

Os atributos de saída também são apenas dois, e correspondem aos atributos de entrada transformados para o espaço da câmera:

• fragP: posição do vértice no espaço da câmera;
• fragN: vetor normal no espaço da câmera.

Com esses atributos, podemos calcular o vetor de reflexão no fragment shader e então amostrar o mapa de textura cúbico.

cubereflect.frag

O código completo é mostrado a seguir:

#version 300 es

precision mediump float;

in vec3 fragP;
in vec3 fragN;

uniform mat3 texMatrix;
uniform samplerCube cubeTex;

out vec4 outColor;

void main() {
  vec3 V = normalize(-fragP);
  vec3 N = normalize(fragN);
  vec3 R = reflect(-V, N);

  outColor = texture(cubeTex, texMatrix * R);
}

O amostrador do mapa de textura cúbico é definido pela variável cubeTex na linha 9. Observe que o tipo de dado é samplerCube no lugar de sampler2D.

Na linha 14, o vetor V (vetor na direção da câmera) é calculado como -fragP. Como já vimos nos projetos anteriores,

\[ \hat{\mathbf{v}}=\frac{E-P}{|E-P|}, \] e \(E\) é a posição da câmera no espaço da câmera, que é a origem. Logo,

\[ \hat{\mathbf{v}}=\frac{-P}{|-P|}. \]

Na linha 15, o vetor N é fragN normalizado. A normalização é necessária pois, no fragment shader, fragN é o resultado da interpolação linear das coordenadas dos vetores normais definidos nos vértices, e a interpolação linear de dois vetores unitários diferentes entre si não é um vetor unitário.

Na linha 16, o vetor R de reflexão ideal é calculado com a função reflect. O primeiro argumento é -V pois reflect supõe que esse é o vetor incidente em \(P\), e não o vetor que sai de \(P\).

Na linha 18, a função texture é utilizada com o amostrador cubeTex para amostrar o mapa de textura cúbico usando as coordenadas do vetor de reflexão ideal. Como o amostrador é do tipo samplerCube, o OpenGL se encarrega de amostrar o lado correto do cubemap.

Observe que, na chamada a texture, transformamos R pela matriz texMatrix. Essa é a matriz inversa de rotação obtida do trackball virtual m_trackBallLight (trackball usado para mudar a direção da fonte de luz). Com isso podemos simular o efeito de girar o cubo imaginário usando o trackball da fonte da luz. Em Window::onPaint, a variável uniforme texMatrix é definida como:

  glm::mat3 const texMatrix{m_trackBallLight.getRotation()};
  abcg::glUniformMatrix3fv(texMatrixLoc, 1, GL_TRUE, &texMatrix[0][0]);

O segundo argumento de glUniformMatrix3fv é GL_TRUE. Isso faz com que a matriz enviada seja a transposta da original, que é igual à inversa da matriz (lembre-se que matrizes de rotação são ortogonais). Precisamos da matriz inversa, pois rodar o cubo imaginário por, digamos, \(90^\circ\) em torno do eixo \(x\), corresponde a manter o cubo parado e rodar o vetor R por \(-90^\circ\) em torno do mesmo eixo. Só podemos rodar o vetor R, pois o OpenGL não possui uma função para rodar o cubemap.

Isso é tudo para o efeito de reflexão. Vamos agora aos shaders de refração.

cuberefract.vert

O código deste vertex shader é exatamente igual ao código de cubereflect.vert:

#version 300 es

layout(location = 0) in vec3 inPosition;
layout(location = 1) in vec3 inNormal;

uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projMatrix;
uniform mat3 normalMatrix;

out vec3 fragP;
out vec3 fragN;

void main() {
  fragP = (viewMatrix * modelMatrix * vec4(inPosition, 1.0)).xyz;
  fragN = normalMatrix * inNormal;

  gl_Position = projMatrix * vec4(fragP, 1.0);
}

cuberefract.frag

O código do fragment shader também é muito parecido com o código de cubereflect.frag:

#version 300 es

precision mediump float;

in vec3 fragP;
in vec3 fragN;

uniform mat3 texMatrix;
uniform samplerCube cubeTex;

out vec4 outColor;

void main() {
  vec3 V = normalize(-fragP);
  vec3 N = normalize(fragN);
  vec3 T = refract(-V, N, 1.0 / 1.52);  // Air to glass

  outColor = texture(cubeTex, texMatrix * T);
}

A diferença principal em relação ao shader de reflexão está na linha 19: calculamos um vetor T de refração usando a função refract. A função recebe como argumentos o vetor incidente (-V), o vetor normal (N), e a razão entre os índices de refração, que neste caso é 1.0 / 1.52 pois estamos considerando uma transição do ar para o vidro.

Renderizando um skybox

Skybox é o nome dado a um cubo centralizado ao redor da câmera e texturizado com o mapa de textura cúbico de modo a simular uma imagem de fundo.

Para renderizar um skybox, precisamos definir primeiro a geometria do cubo. Na definição da classe Window (em window.hpp), definimos a posição dos vértices de cada lado do cubo em um arranjo m_skyPositions:

  std::array<glm::vec3, 36> const m_skyPositions{{
      // Front
      {-1, -1, +1}, {+1, -1, +1}, {+1, +1, +1},
      {-1, -1, +1}, {+1, +1, +1}, {-1, +1, +1},
      // Back
      {+1, -1, -1}, {-1, -1, -1}, {-1, +1, -1},
      {+1, -1, -1}, {-1, +1, -1}, {+1, +1, -1},
      // Right
      {+1, -1, -1}, {+1, +1, -1}, {+1, +1, +1},
      {+1, -1, -1}, {+1, +1, +1}, {+1, -1, +1},
      // Left
      {-1, -1, +1}, {-1, +1, +1}, {-1, +1, -1},
      {-1, -1, +1}, {-1, +1, -1}, {-1, -1, -1},
      // Top
      {-1, +1, +1}, {+1, +1, +1}, {+1, +1, -1},
      {-1, +1, +1}, {+1, +1, -1}, {-1, +1, -1},
      // Bottom
      {-1, -1, -1}, {+1, -1, -1}, {+1, -1, +1},
      {-1, -1, -1}, {+1, -1, +1}, {-1, -1, +1}}};

O cubo será renderizado com GL_TRIANGLES sem usar geometria indexada. Assim, cada lado do cubo é formado por dois triângulos, e cada triângulo é uma sequência de três vértices do tipo glm::vec3.

Podemos definir coordenadas de textura para cada lado do cubo e então renderizar cada lado com a textura correspondente do mapa de textura cúbico. Entretanto, isso não é necessário. Podemos usar diretamente a posição dos vértices como coordenadas de amostragem do amostrador samplerCube.

Precisamos de um VBO (m_skyVBO), VAO (m_skyVAO), e um programa de shader (m_skyProgram) para renderizar o cubo. Em Window, adicionamos os seguintes membros da classe:

  std::string const m_skyShaderName{"skybox"};
  GLuint m_skyVAO{};
  GLuint m_skyVBO{};
  GLuint m_skyProgram{};

m_skyShaderName é o nome dos arquivos dos shaders: skybox.vert e skybox.frag.

Os recursos (VBO, VAO, etc) são inicializados na função Window::createSkybox chamada em Window::onCreate:

void Window::createSkybox() {
  auto const assetsPath{abcg::Application::getAssetsPath()};

  // Create skybox program
  auto const path{assetsPath + "shaders/" + m_skyShaderName};
  m_skyProgram = abcg::createOpenGLProgram(
      {{.source = path + ".vert", .stage = abcg::ShaderStage::Vertex},
       {.source = path + ".frag", .stage = abcg::ShaderStage::Fragment}});

  // Generate VBO
  abcg::glGenBuffers(1, &m_skyVBO);
  abcg::glBindBuffer(GL_ARRAY_BUFFER, m_skyVBO);
  abcg::glBufferData(GL_ARRAY_BUFFER, sizeof(m_skyPositions),
                     m_skyPositions.data(), GL_STATIC_DRAW);
  abcg::glBindBuffer(GL_ARRAY_BUFFER, 0);

  // Get location of attributes in the program
  auto const positionAttribute{
      abcg::glGetAttribLocation(m_skyProgram, "inPosition")};

  // Create VAO
  abcg::glGenVertexArrays(1, &m_skyVAO);

  // Bind vertex attributes to current VAO
  abcg::glBindVertexArray(m_skyVAO);

  abcg::glBindBuffer(GL_ARRAY_BUFFER, m_skyVBO);
  abcg::glEnableVertexAttribArray(positionAttribute);
  abcg::glVertexAttribPointer(positionAttribute, 3, GL_FLOAT, GL_FALSE, 0,
                              nullptr);
  abcg::glBindBuffer(GL_ARRAY_BUFFER, 0);

  // End of binding to current VAO
  abcg::glBindVertexArray(0);
}

Também definimos a função Window::destroySkybox que é chamada em Window::onDestroy para liberar os recursos:

void Window::destroySkybox() const {
  abcg::glDeleteProgram(m_skyProgram);
  abcg::glDeleteBuffers(1, &m_skyVBO);
  abcg::glDeleteVertexArrays(1, &m_skyVAO);
}

Para renderizar o cubo, definimos a função Window::renderSkybox que é chamada em Window::onPaint depois da renderização do objeto que está sendo visualizado:

void Window::renderSkybox() {
  abcg::glUseProgram(m_skyProgram);

  auto const viewMatrixLoc{
      abcg::glGetUniformLocation(m_skyProgram, "viewMatrix")};
  auto const projMatrixLoc{
      abcg::glGetUniformLocation(m_skyProgram, "projMatrix")};
  auto const skyTexLoc{abcg::glGetUniformLocation(m_skyProgram, "skyTex")};

  auto const viewMatrix{m_trackBallLight.getRotation()};
  abcg::glUniformMatrix4fv(viewMatrixLoc, 1, GL_FALSE, &viewMatrix[0][0]);
  abcg::glUniformMatrix4fv(projMatrixLoc, 1, GL_FALSE, &m_projMatrix[0][0]);
  abcg::glUniform1i(skyTexLoc, 0);

  abcg::glBindVertexArray(m_skyVAO);

  abcg::glActiveTexture(GL_TEXTURE0);
  abcg::glBindTexture(GL_TEXTURE_CUBE_MAP, m_model.getCubeTexture());

  abcg::glEnable(GL_CULL_FACE);
  abcg::glFrontFace(GL_CW);
  abcg::glDepthFunc(GL_LEQUAL);
  abcg::glDrawArrays(GL_TRIANGLES, 0, m_skyPositions.size());
  abcg::glDepthFunc(GL_LESS);

  abcg::glBindVertexArray(0);
  abcg::glUseProgram(0);
}

Observe como a matriz de visão é a matriz de rotação do trackball da fonte de luz (m_trackBallLight). Assim, conseguimos rodar o cubo através desse trackball.

Como a câmera está dentro do cubo, o back-face culling é ativado (linha 478) considerando que o lado da frente das faces tem orientação horária (linha 479), isto é, o lado da frente é o lado voltado para dentro do cubo.

Na linha 480, a função de comparação do teste de profundidade é modificada para GL_LEQUAL (menor ou igual a) no lugar da configuração padrão GL_LESS (menor que). Isso é necessário pois, no shader, faremos com que a posição de cada fragmento tenha valor máximo de profundidade (\(z=1\) em NDC) para que somente os pixels “mais distantes” do framebuffer sejam modificados. Na configuração padrão, glClear limpa os pixels do buffer de profundidade com valor 1. Assim, após a renderização do objeto, os pixels com valor 1 correspondem aos pixels que ainda não foram modificados, e somente esses pixels precisam ser desenhados com a textura de fundo. A função GL_LEQUAL garante que esses pixels serão preenchidos com o skybox.

No lugar de modificar a função de teste de profundidade e renderizar o cubo com \(z=1\) em NDC, poderíamos simplesmente renderizar o cubo primeiro, sem modificar o buffer de profundidade, e então renderizar o objeto por cima. Entretanto, a abordagem que adotamos (desenhar o cubo depois do objeto) é mais eficiente pois evita sobreposições de pixels e permite que o pipeline não perca tempo processando fragmentos que não passarão no teste de profundidade.

Os shaders skybox.vert e skybox.frag são definimos a seguir.

skybox.vert

#version 300 es

layout(location = 0) in vec3 inPosition;

out vec3 fragTexCoord;

uniform mat4 viewMatrix;
uniform mat4 projMatrix;

void main() {
  fragTexCoord = inPosition;

  vec4 P = projMatrix * viewMatrix * vec4(inPosition, 1.0);
  gl_Position = P.xyww;
}

O atributo de entrada do vertex shader é a posição do vértice do cubo (inPosition).

O atributo de saída é fragTexCoord, que corresponde às coordenadas que serão utilizadas para amostrar o mapa de textura cúbico. Na linha 11, essas coordenadas são definidas com os valores de inPosition, isto é, a posição do vértice é considerada como as coordenadas do vetor que será utilizado para amostrar a textura.

Na linha 13, P é a posição do vértice transformada para o espaço de recorte.

Na linha 14, utilizamos um pequeno truque: definimos gl_Position como P.xyww, que corresponde a um vetor no qual o valor da coordenada \(w\) é repetido como valor da coordenada \(z\). Ao fazer isso, garantimos que \(z\) será sempre 1 em NDC, pois a divisão por \(w\) feita após o recorte dividirá \(z\) por \(w\). Como ambos têm o mesmo valor, o resultado será 1. Com isso conseguimos fazer parecer que as faces do cubo estão sempre no fundo da cena.

skybox.frag

#version 300 es

precision mediump float;

in vec3 fragTexCoord;

out vec4 outColor;

uniform samplerCube skyTex;

void main() { outColor = texture(skyTex, fragTexCoord); }

O fragment shader recebe a saída do vertex shader (fragTexCoord), que são as coordenadas utilizadas para amostrar o mapa de textura cúbido através do amostrador skyTex.

Observação

Como o OpenGL define o cubo imaginário do mapeamento cúbico em um espaço que segue a regra da mão esquerda, a imagem de fundo do skybox normalmente ficaria espelhada em relação ao que é mostrado na figura 10.29. Isso só não ocorre porque a função abcg::loadOpenGLCubemap corrige automaticamente as texturas para nós. A correção é feita trocando a textura +z com a textura -z, virando +y e -y de cabeça para baixo, e virando as demais texturas horizontalmente. Consulte o código da função para mais detalhes.